LESSON MENSURATION
1. क्षेत्रमिति की परिचय बताये है ?
दोस्तों क्षेत्रमिति में परिमिति, क्षेत्रफल, आयतन, आदि की माप के बारे में अध्ययन किया जाता है। और इससे जुड़े सवाल आपको प्रायः प्रत्येक प्रतियोगी परीक्षा में जरुर पूछा जाता हैं।
तो आज के इस लेख में आप इसी के बारे में जानेगे | तो चलिये, शुरू करते है, आज का अध्याय...
☆ यदि किसी आयत के आसन्न भुजाओं में एक को शांत रखकर दुसरे को अगर K से गुणा किया जाये तो आयत का प्राप्त क्षेत्रफल K गुणा हो जायेगा |
☆ यदि किसी आयत के आसन्न भुजाओं में एक को शांत रखकर दुसरे को अगर K% से बढ़ाया जाये या फिर घटाया जाये, तो आयत का प्राप्त क्षेत्रफल भी K% से क्रमशः बढेगा या फिर घटेगा |
♥ क्षेत्रमिति विषय लेख के मुख्य बिंदुओ...
1. क्षेत्रमिति की परिचय बताये है ?
2. क्षेत्रमिति आकृतियों को एक - एक कर समझाये !
2. क्षेत्रमिति आकृतियों को एक - एक कर समझाये !
दोस्तों यहाँ पर मैं आपको इस लेख में क्षेत्रमिति के अंतर्गत आने वाले सभी द्विविमीय या त्रिविमीय आकृतियों के क्षेत्रफल, परिमाप, आयतन आदि का के बारे में जानेगे तथा इसके सूत्र को भी जानेगे तो सबसे पहले द्विविमीय आकृतियाँ (Two Dimensional Figures) के बारे में एक - एक कर जानेगे |
☆ आयत (Rectangle)
परिभाषा:- जिसकी आमने - सामने की भुजा आपस में बराबर हो, उसे आयत कहते है |आयत का क्षेत्रफल = लम्बाई × चौड़ाई
आयत का परिमिति = 2 (लम्बाई + चौड़ाई)
आयत का विकर्ण = लम्बाई²+चौड़ाई²
☆ अगर आयत का क्षेत्रफल दिया हुआ है, तो ...
 आयत का लम्बाई =
आयत का लम्बाई = क्षेत्रफल/चौड़ाई
आयत का चौड़ाई =
क्षेत्रफल/लम्बाई
☆ अगर आयत का परिमिति दिया हुआ है, तो ...
आयत का लम्बाई =
परिमिति/चौड़ाई
आयत का चौड़ाई =
परिमिति/लम्बाई
☆ वर्ग (Square)
 परिभाषा:- जिसकी चारों भुजा आपस में बराबर हो, उसे वर्ग कहते है |
परिभाषा:- जिसकी चारों भुजा आपस में बराबर हो, उसे वर्ग कहते है |वर्ग का क्षेत्रफल = (भुजा) ²
वर्ग का परिमिति = 4 × भुजा
वर्ग का विकर्ण = × भुजा
वर्ग की लम्बाई =
परिमिति/4
वर्ग की भुजा =
☆ त्रिभुज (Triangle)
परिभाषा:- तिन रेखाओं घेरे से घिरी हुई आकृति को त्रिभुज वर्ग कहते है |त्रिभुज का क्षेत्रफल =
1/2
× आधार × ऊँचाई 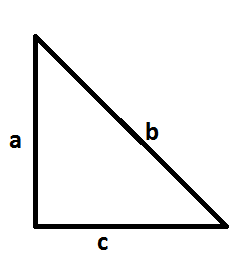 विषमबाहु त्रिभुजः यदि a, b तथा c क्रमशः पहली, दूसरी और तीसरी भुजा की लम्बाईयाँ हो तब
(s = अर्ध-परिमिति) = जहाँ S =
विषमबाहु त्रिभुजः यदि a, b तथा c क्रमशः पहली, दूसरी और तीसरी भुजा की लम्बाईयाँ हो तब
(s = अर्ध-परिमिति) = जहाँ S = a+b+c/2
और, क्षेत्रफल =
समकोण त्रिभुज
यदि त्रिभुज समकोण हो, तब क्षेत्रफल =
आधार × लम्ब/2
समबाहु त्रिभुज

समबाहु त्रिभुज का क्षेत्रफल =
/4
a²समबाहु त्रिभुज की परिमिति = 3a या 3 × एक भुजा
क्षेत्रफल = π × (त्रिज्या)²
परिधि = 2π × त्रिज्या
त्रिज्या =
समद्दीबाहू समकोण त्रिभुज
समद्दीबाहू समकोण त्रिभुज का क्षेत्रफल =
1/2
× भुजा ²☆ वृत (Circle)
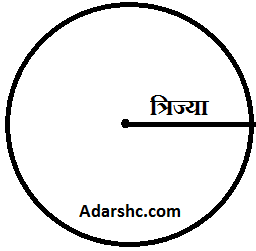 परिभाषा:- गोल घेरे से घिरी हुई आकृति को वृत वर्ग कहते है |
परिभाषा:- गोल घेरे से घिरी हुई आकृति को वृत वर्ग कहते है |वृत का क्षेत्रफल = π × (त्रिज्या)²
वृत की परिधि = 2π × त्रिज्या
वृत की त्रिज्या r =
वृत की त्रिज्या =
वृत की परिधि/2π
वृत का' व्यास =
परिधि/π
☆ अर्द्ध-वृत (Semicircle)
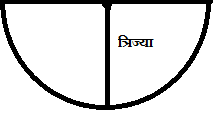 परिभाषा:- गोल घेरे से घिरी हुई आकृति को वृत वर्ग कहते है |
परिभाषा:- गोल घेरे से घिरी हुई आकृति को वृत वर्ग कहते है |अर्द्ध-वृत का क्षेत्रफल =
1/2
× πr²अर्द्ध-वृत की परिमिति = πr या
πd/2
जहाँ r = त्रिज्या और d = व्यास☆ चतुर्भुज (Quadrilateral)
☆ समांतर चतुर्भुज (Parallelogram)
 समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाईसमांतर चतुर्भुज का आधार =
क्षेत्रफल/ऊँचाई
समांतर चतुर्भुज का ऊँचाई =
क्षेत्रफल/आधार
समांतर चतुर्भुज की परिमिति = 2 × (आसन्न भुजाओं का योग)
समांतर चतुर्भुज की पहली आसन्न भुजा =
परिमिति/2
- दूसरी आसन्न भुजासमांतर चतुर्भुज की दूसरी आसन्न भुजा =
परिमिति/2
- पहली आसन्न भुजासमांतर चतुर्भुज का क्षेत्रफल = विकर्ण × शीर्ष से विकर्ण की ल्म्बात्मक दूरी
☆ समचतुर्भुज (Rhombus)
 समचतुर्भुज का क्षेत्रफल = 1/2 × विकर्णों का गुणनफल
समचतुर्भुज का क्षेत्रफल = 1/2 × विकर्णों का गुणनफल☆ समलम्ब चतुर्भुज
समलम्ब चतुर्भुज क्षेत्रफल = 1/2 × (समान्तर भुजाओं का योग) × उनके बीच की दूरीविषमबाहु चतुर्भुज क्षेत्रफल = ½ (DP + BQ) × AC
☆ त्रिविमीय आकृतियाँ (Three dimensional Figures)
☆ घनाभ (Cuboid)
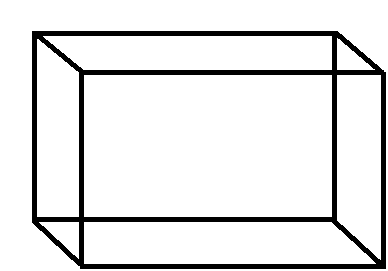 यदि घनाभ की लम्बाई, चौड़ाई तथा ऊँचाई क्रमशः L, B और H हो तब घनाभ का आयतन = L × B × H
यदि घनाभ की लम्बाई, चौड़ाई तथा ऊँचाई क्रमशः L, B और H हो तब घनाभ का आयतन = L × B × Hसम्पूर्ण पृष्ठ का क्षेत्रफल = 2 (L × B + B × H + H × L)
☆ घन (Cube)
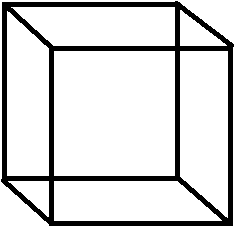 यदि घन की प्रत्येक भुजा a हो, तब घन का आयतन = a × a × a = a³
यदि घन की प्रत्येक भुजा a हो, तब घन का आयतन = a × a × a = a³सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a²
☆ बेलन (Cylinder)
 यदि बेलन की त्रिज्या r तथा ऊँचाई या लम्बाई h हो, तब बेलन का आयतन = πr²h
यदि बेलन की त्रिज्या r तथा ऊँचाई या लम्बाई h हो, तब बेलन का आयतन = πr²hबेलन का वक्र पृष्ठ क्षेत्रफल = 2πrh
बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल = 2πr(h + r)
☆ शंकु (Cone)
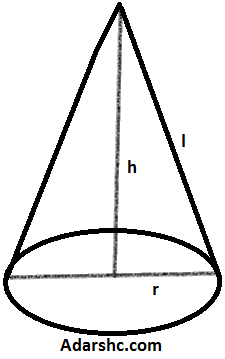 यदि शंकु के आधार की त्रिज्या, ऊँचाई तथा इसकी तिर्यक-ऊँचाई क्रमशः r, h तथा ℓ हो, तब:
शंकु का आयतन =
यदि शंकु के आधार की त्रिज्या, ऊँचाई तथा इसकी तिर्यक-ऊँचाई क्रमशः r, h तथा ℓ हो, तब:
शंकु का आयतन = 1/3
πr²h
शंकु वक्र-पृष्ठ का क्षेत्रफल = πrℓ
शंकु सम्पूर्ण पृष्ठ का क्षेत्रफल = πr(ℓ + r)
☆ गोला (Sphere)
 यदि गोले की त्रिज्या r हो, तब आयतन =
यदि गोले की त्रिज्या r हो, तब आयतन = 4/3
πr³गोला वक्र-पृष्ठ क्षेत्रफल = 4πr²
☆ अर्द्ध-गोला (Semisphere)
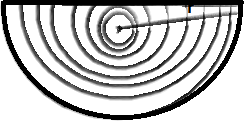 अर्द्ध-गोला का आयतन =
अर्द्ध-गोला का आयतन = 2/3
πr²अर्द्ध-गोला का वक्र-पृष्ठ क्षेत्रफल = 2πr²
अर्द्ध-गोला का सम्पूर्ण पृष्ठ क्षेत्रफल = 3πr²



Comments are as...
☆ Leave Comment...