LESSON Trigonometry
त्रिकोणमिति (Trigonometry)
 दोस्तों आज के अध्याय में आप त्रिकोणमिति से जुडी जानकारियाँ प्राप्त करने वाले है |
दोस्तों आज के अध्याय में आप त्रिकोणमिति से जुडी जानकारियाँ प्राप्त करने वाले है | आपको इस लेख के अंतर्गत इसके बारे परिचय दिया जायेगा , इससे जुड़े हुये तस्वीरों की मदद से भी समझाने का प्रयास करेंगे,
और इसके साथ - साथ आप इसके सभी सूत्रों को एक जगह तथा एक सही तरीके से सजाया हुआ आप प्राप्त करेंगे |
जिससे की आपको किसी भी सूत्र को पढ़ने और समझने में कोई परेशानी नहीं होगी |
तो चलिये आज का लेख शुरू करते है...
♥ प्रतिशत विषय लेख के मुख्य बिंदुओ...
1. त्रिकोणमिति की परिभाषा क्या है ?
2. त्रिकोणमिति संबंध या अनुपात बताये !
3. त्रिकोणमिति फलन या अनुपात का महत्वपूर्ण तथ्य !
4. त्रिकोणमिति फलन या अनुपात का महत्वपूर्ण सूत्र !
5. त्रिकोणमिति पादों के महत्वपूर्ण सूत्र !
1. त्रिकोणमिति की परिभाषा क्या है ?
गणित की वह शाखा जिसके अंतर्गत त्रिभुज के कोणों और भुजाओं का अधयन्न किया जाता है, उसे त्रिकोणमिति कहा जाता है |
☆ त्रिकोणमिति के साधारण सूत्र को समझने के लिये आप इस तस्वीर की मदद से समझ सकते है..
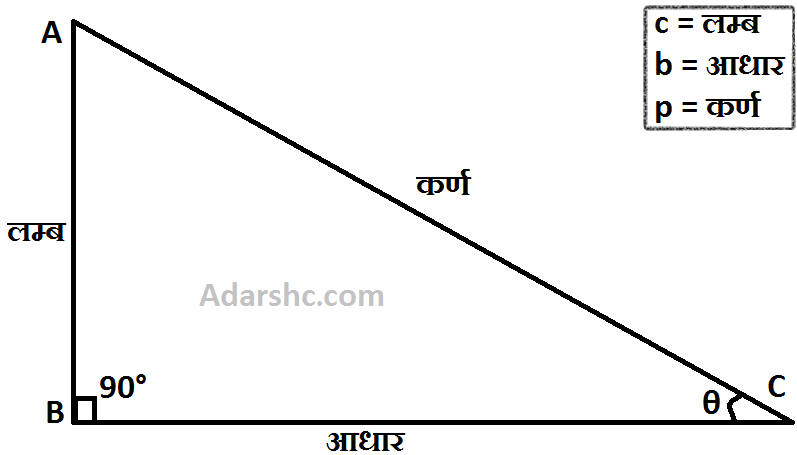
BC = आधार = b
AB = लम्ब = p
1. कर्ण² = लम्ब² + आधार²
या इसे आप इस प्रकार से भी चित्र के अनुसार लिख सकते है..
AC² = AB² + BC²
2. लम्ब² = कर्ण² - आधार² या AB² = AC² - BC²
3. आधार² = कर्ण² - लम्ब² या BC² = AC² - AB²
2. त्रिकोणमिति संबंध या अनुपात बताये !
त्रिकोणमिति संबंध या अनुपात निम्न प्रकार से है...
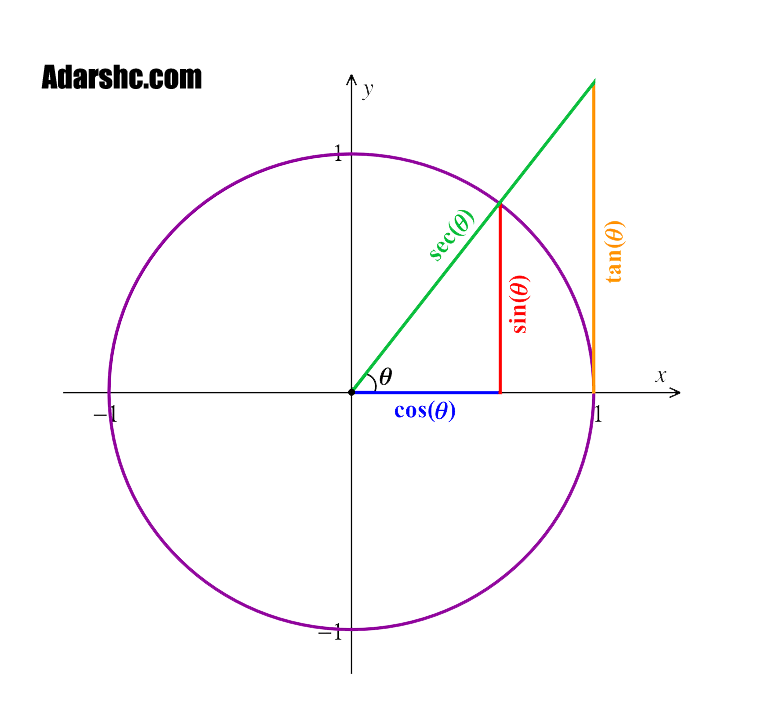
1. sinθ =
2. cosθ =
3. tanθ =
लम्ब/कर्ण
=
AB/AC
2. cosθ =
आधार/कर्ण
=
BC/AC
3. tanθ =
लम्ब/आधार
=
AB/BC
4. cotθ =
5. secθ =
6. cosecθ =
आधार/लम्ब
=
BC/AB
5. secθ =
कर्ण/आधार
=
AC/BC
6. cosecθ =
कर्ण/लम्ब
=
AC/AB
3. त्रिकोणमिति फलन या अनुपात का महत्वपूर्ण तथ्य !
☆ sinθ.cosθ.tanθ.cotθ.secθ.cosecθ इन सभी को त्रिकोणमिति फलन, निष्पति या अनुपात कहा जाता है|
☆ प्रत्येक त्रिकोणमिति फलन दो चीजों का बना हुआ होता है, जिसके अंतर्गत पहला वृतीय फलन तथा दूसरा चर कोण होते है |
☆ sinθ को वृतीय फलन कहा जाता है, जिसमें θ एक Variable कोण है |
तथा ठीक इसी प्रकार अन्य सभी पाचों में एक त्रिकोणमिति फलन तथा एक Variable कोण होता है |
त्रिकोणमिति फलनों के बिच प्रारंभिक संबंध..
♥ sin A =
♥ cosec A =
♥ cos A =
♥ sin A =
1/sin A
♥ cosec A =
1/cosec A
♥ cos A =
1/sec A
♥ sin A =
1/cos A
♥ tan A =
♥ cot A =
♥ tan A =
♥ cot A =
1/cot A
♥ cot A =
1/tan A
♥ tan A =
sin A/cos A
♥ cot A =
cos A/sin A
♥ sin A × cosec A = 1
♥ cos A × sec A = 1
♥ tan A × cot A = 1
♥ cos A × sec A = 1
♥ tan A × cot A = 1
4. त्रिकोणमिति फलन या अनुपात का महत्वपूर्ण सूत्र !
a. sin²θ = 1 - cos²θ
b. cos²θ = 1 - sin²θ
c. sinθ =
d. cosθ =
Note :-
a. में जो सूत्र आप देख रहे उसे बनाने के लिये आपको सिर्फ cos²θ बराबर (=) चिन्ह के उस पार ले जाते है, तो चिन्ह में परिवर्तन किया गया है, + था, तो = के पार जाने पर - चिन्ह हो जायेगा |b. में जो सूत्र आप देख रहे उसे बनाने के लिये आपको सिर्फ sin²θ + cos²θ = 1 में से अबकी बार sin²θ को बराबर (=) चिन्ह के उस पार ले जाते है, तो चिन्ह में परिवर्तन किया गया है, + था, तो = के पार जाने पर - चिन्ह हो जायेगा |
c. में जो सूत्र आप देख रहे उसे बनाने के लिये sin²θ = 1 - cos²θ में से sin²θ से स्क्वायर हटाने पर = चिन्ह के उस पार वाले सभी रूट के अंदर आयेगे |
d. में जो सूत्र आप देख रहे उसे बनाने के लिये cos²θ = 1 - sin²θ में से cos²θ से स्क्वायर हटाने पर = चिन्ह के उस पार वाले सभी रूट के अंदर आयेगे |
☆ ठीक इसी नियम के आधार पर निचे के सभी सूत्र बनाये जा सकते है, और मैं तो कहूँगा की इसे रटने से अच्छा है, की आप इसे अच्छी तरह से समझ ले
 2. tan²θ - sec²θ = 1
2. tan²θ - sec²θ = 1tan²θ = 1 + sec²θ
sec²θ = tan²θ - 1
tanθ =
secθ =
3. cosec²θ - cot²θ = 1
cosec²θ = 1 + cot²θ
cot²θ = 1 - cosec²θ
cosecθ =
cotθ =
5. त्रिकोणमिति पादों के महत्वपूर्ण सूत्र !
| अनुपात | 0° | 30° | 45° | 60° | 90° |
| sinθ | 0 | 1/2 |
1/ |
/2 |
1 |
| cosθ | 1 | /2 |
1/ |
1/2 |
0 |
| tanθ | 0 | 1/ |
1 | ∞ | |
| cotθ | ∞ | 1 | 1/ |
0 | |
| secθ | 1 | 2/ |
2 | ∞ | |
| cosecθ | ∞ | 2 | 2/ |
1 |



Comments are as...
☆ Leave Comment...